Несколько задач с ВСО 2017 по компьютерной безопасности

Довелось мне быть на Всероссийской студенческой олимпиаде, где юные пытливые умы со всей России показывали свои навыки в криптологии, защите информации, reverse-ingeneer’инге и других презабавных вещах. Удивительно было, ни капли не готовясь и будучи только на втором курсе, стать лауреатом, и вообще было парадоксально, что вылез вперед я не благодаря практике (которую, как лох, завалил), а теории. Посему хочу поделиться решениями некоторых задачек по криптологии, которые мне показались интересными я правильно решил.

1. Лдрисд + аквонатсереп

Пусть А – это шифр моноалфавитой замены, В – шифр перестановки. Дан блок длины n. АВ значит, что сначала применяем шифр В, а затем А. Будет ли АВ=ВА? Насколько изменится сложность дешифровки, если вместо АВ использовать АВАВ?

Решение: Определим для начала шифр перестановки в блоке и шифр простой замены (эквивалентно "моноалфавитному"). Как это сделать, можно посмотреть в документе.

Теперь, когда мы все это определили, можно расписать применение AB и ВА.

Пусть $$X=(x_1, x_2, ... x_n)$$  – это блок, который нужно зашифровать.

$$А=E(X)=(E(x_1), E(x_2), E(x_3), ..., E(x_n))=(y_1, y_2, y_3, ... , y_n) = Y$$ – это операция шифрования простой замены.

$$B=\tilde E (X) = (x_{\tilde E (1)}, x_{\tilde E (2)}, x_{\tilde E (3)}, ..., x_{\tilde E (n)})=(z_1, z_2, z_3, ... , z_n) = Z$$ – это операция шифрования перестановки в блоке. Нужно пояснить, что определена она как подстановка номеров, поэтому мы можем выполнить ее как бы на индексах.

$$AB=E(\tilde E (X) )= E(Z) = (E(z_1), E(z_2), E(z_3), ..., E(z_n)) = \\ =(E(x_{\tilde E (1)}), E(x_{\tilde E (2)}), E(x_{\tilde E (3)}), ..., E(x_{\tilde E (n)})) $$ – применяем АВ

$$BA = \tilde E (E(X)) = \tilde E (Y) = (y_{\tilde E (1)}, y_{\tilde E (2)}, y_{\tilde E (3)}, ..., y_{\tilde E (n)}) = \\ = (E(x_{\tilde E (1)}), E(x_{\tilde E (2)}), E(x_{\tilde E (3)}), ..., E(x_{\tilde E (n)})) $$ – применяем ВА. Может возникнуть резонный вопрос, почему мы применили операцию к индексам Y, а получили другие индексы у X. Потому что подстановка индексов взаимно однозначна (см. определение шифра математически).

Итак, получили, что $$\tilde E (E(X)) = E(\tilde E (X) )$$ или BA=AB.

Теперь рассмотрим АВАВ.

После применения шифров изменятся замены и перестановки. ОДНАКО:

1) Не изменятся частоты встречаемости букв

2) "Перестановка изменится" означает всего лишь другой ключ

Поэтому для вскрытия шифра АВАВ потребуются те же действия (частотный анализ и анализ для шифра перестановки в блоке), что и для шифра АВ. Таким образом, если мы применим АВАВ (Ну, или даже АВАВ...АВАВ) сложность вскрытия не изменится.

2. Бдительный арбитр

Придумайте систему анонимного электронного голосования, при котором каждый его участник сможет доказать арбитру, что его голос не искажен.

Решение: Самое главное в условии, что голосование должно быть (и оставаться впоследствие) анонимным, и что каждый участник сможет доказать неизменность своего голоса.

Давайте дадим каждому участнику какой-нибудь секретный ключик, который знают только они сами. Назовем его secretkey.

Итак, у каждого участника есть свои ключики secretkey(i). Участник под условным номером iрешает проголосовать за вариант var(i). Он нажимает на необходимую кнопку, и тут же происходит несколько действий.

1) Вычисляется X(i)= md5( var(i) + secret(i) ), и вектор { var(i), X(i)} отправляется на сервер.

2) На экране устройства голосующего появляется (или печатается) результат выполнения функции Z(i) = md5( var(i) + X(i) ) 

Пришедший на сервер вектор лежит в базе голосования (var(i) используется для подсчета голосов), а на компуктер арбитра отправляется md5( Var(i) + X(i)) , где Var(i) - то, что использовалось при подсчете голосов. Необязательно Var(i)=var(i).

Арбитр имеет доступ к обезличенным хешам, по которым нельзя сопоставить голосующего с его голосом. И он может подойти к любому человеку для проверки того, что вывелось (напечаталось) на его устройстве. Если Z(i) пользователя существует в базе арбитра, значит голос пользователя не искажен, иначе грусть, и выборы президента Америки взломали русские хацкеры.

Схема может выглядеть так:

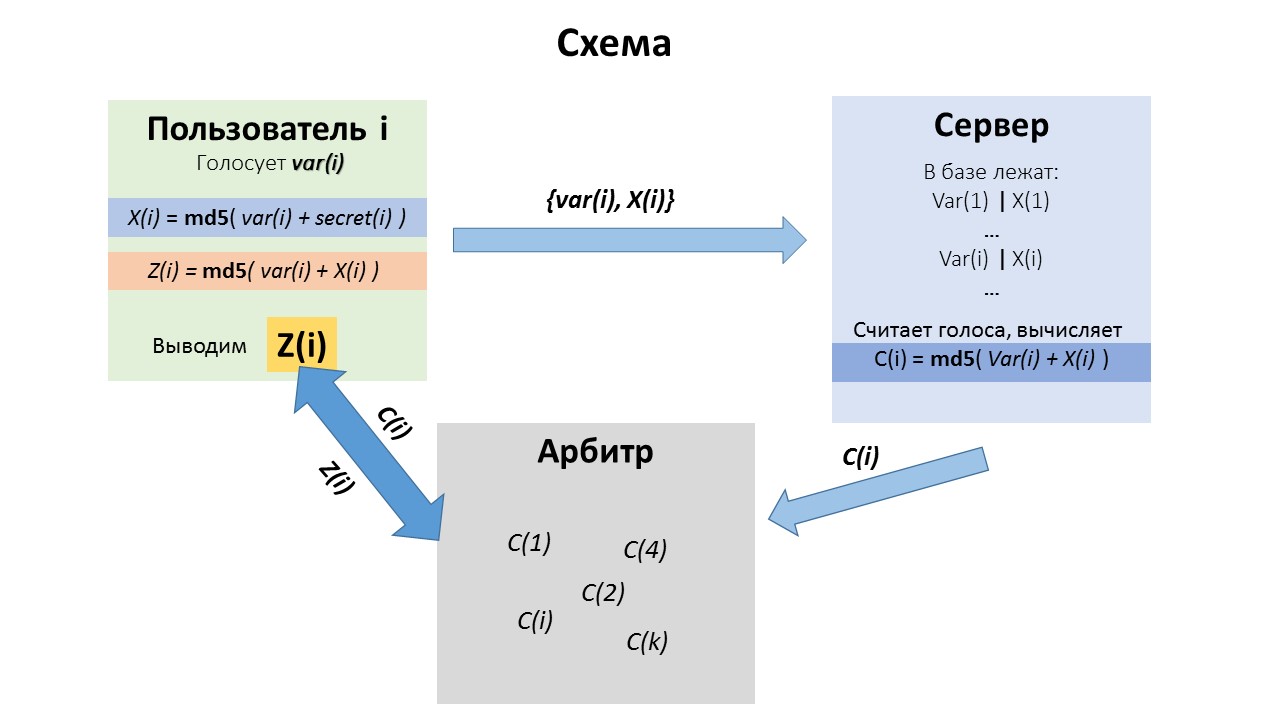
Получается, можно проверить, учтен ли верный голос пользователя и нельзя лишить его анонимности.

3. Шифр md5 (WAT?!)

Составить блочный шифр на основе md5.

Решение: Блок у нас размером m, m<33 (Так как md5() выдает 32 символа)

Пусть Получатель (П) и Отправитель (О) договорились о ключе К.

Тогда чтобы зашифровать послание P, О должен разделить послание на блоки до 32 символов, вычислить $$ EncKey=md5(K) $$ , а затем $$ Encrypted = P(i) \oplus EncKey$$, где i пробегает все части послания.

Чтобы расшифровать Encrypted, П необходимо разделить послание на блоки до 32 символов (размер обговаривается с О), вычислить $$ EncKey=md5(K) $$, а затем $$ Decrypted = Encrypted(i) \oplus EncKey$$, где i пробегает все части шифр-послания.

Пример:

Шифруем $$ P =    101110110...01 $$

Пусть $$  md5(K) = 110100100...11 = EncKey $$

$$ Encrypted =  ( 1+1 mod 2, 0+1 mod 2 , ... ) = 011010010...10 $$

$$ Decrypted =  (0+1 mod 2, 1+1 mod 2, ... ) = 101110110...01 $$

$$ Encrypted = Decrypted $$

Ну, вот, как-то так =)